پاسکال - مثلث خیام پاسکال

مثلث خیام پاسکال

در قرن ۱۶ میلادی ریاضی‌دان ایتالیایی تارتالیا هم از خود این مثلث را به جا گذاشته و پس از یک قرن پاسکال ریاضی‌دان فرانسوی هم دوره با نیوتن روی این بسط و مثلث حسابی آن کار کرد. مثلث سرپینسکی حاوی کپی هایی کوچک تر از خود است و می دانیم فراکتال شکل هندسی چند جزئی است که می‌توان آن را به قسمت هایی تقسیم کرد، به طوری که هر قسمت یک کپی از "کل" شکل باشد. در واقع اولین عدد مثلثی مساوی است با مجموع یک عدد از اعداد طبیعی، دومین معادل است با مجموع دو عدد از اعداد طبیعی، سومین معادل است با مجموع سه عدد از اعداد طبیعی و. راجع به این که دانشمندان مختلف به صورت مستقل و بدون آگاهی از کارهای قبل از خودشان به کشف این مثلث رسیده‌اند یا نه اختلافات تاریخی ممکن است وجود داشته باشد.

کتاب مشکلات الحساب، کتابی که اثبات‌های این ادعا در آن آمده هنوز کشف نشده ولی در آثار طوسی تأثیر گرفته از او ضرایب را تا توان ۱۲ می‌توان دید. این مثلث توسط دانشمندان گوناگونی از هند و ایران و چین و غیره و بعدتر در اروپا بررسی شده‌است و در زبان‌های گوناگون نام‌های مختلفی دارد. اگر به جای a و b عدد یک را بگذاریم چه اتفاقی می افتد؟ خاصیت جالب بعدی این است که مجموع اعداد هر سطر از مثلث، یکی از توانهای عدد 2 است: . به عنوان مثال پینگالا از هند و عمر خیام از ایران در زمان مشابهی اولین استفاده‌ها از این مثلث را در رساله‌های خود بکار برده‌اند.   این موارد نشان می‌دهد که ممکن است به لخاظ تاریخ علم برخی اعتقاد به کشف مستقل این مثلث از سوی دانشمندان مختلف داشته باشند.

به عنوان مثال در آثار خواجه نصیر الدین طوسی از مثلث خیام پاسکال برای محاسبه‌ی ضرایب بسط یک عبارت جبری استفاده شده است. یکی از زیباترین خواص این مثلث آن است که اگر اعداد هر سطر را چسبیده به هم بنویسیم، اعداد حاصل توانهای 11 خواهند بود:. بعد از عمر خیام، در قرن 12 میلادی، در آثار یانگ هویی (ریاضی دان چینی) نیز ساختار عددی مثلث خیام پاسکال دیده شده است. یکی دیگر از کاربردهای این مثلث که در کتاب ریاضی دهم برای به وجود آمدن اعداد مثلثی در قطر مثلث خیام پاسکال می باشد. در همان دوران عمر خیام ریاضی‌دان ایرانی ادعای کشف روشی جبری برای به دست آوردن ضرایب بسط دوجمله‌ای می‌کند.

مثلث خیام ـ پاسکال، مثلث همه کاره

در قرن ۱۶ میلادی ریاضی دان ایتالیایی تارتالیا هم از خود این مثلث را به جا گذاشته و پس از یک قرن پاسکال ریاضی دان فرانسوی هم دوره با نیوتن روی این بسط و مثلث حسابی آن کار کرد. کتاب «مشکلات الحساب»، کتابی که اثبات های این ادعا در آن آمده هنوز کشف نشده ولی در آثار طوسی تاثیر گرفته از او ضرایب را تا توان ۱۲ می توان دید. در زبان انگلیسی «مثلث پاسکال»، در زبان ایتالیایی «مثلث تارتالیا» و در زبان چینی «مثلث یانگ هویی» نام گرفته است. در همان دوران عمر خیام ریاضی دان ایرانی ادعای کشف روشی جبری برای به دست آوردن ضرایب بسط دوجمله ای می کند. در آثار متون سانسکریت پینگالا ریاضی دان هندی نشانه هایی از استفاده از این بسط دیده می شود.

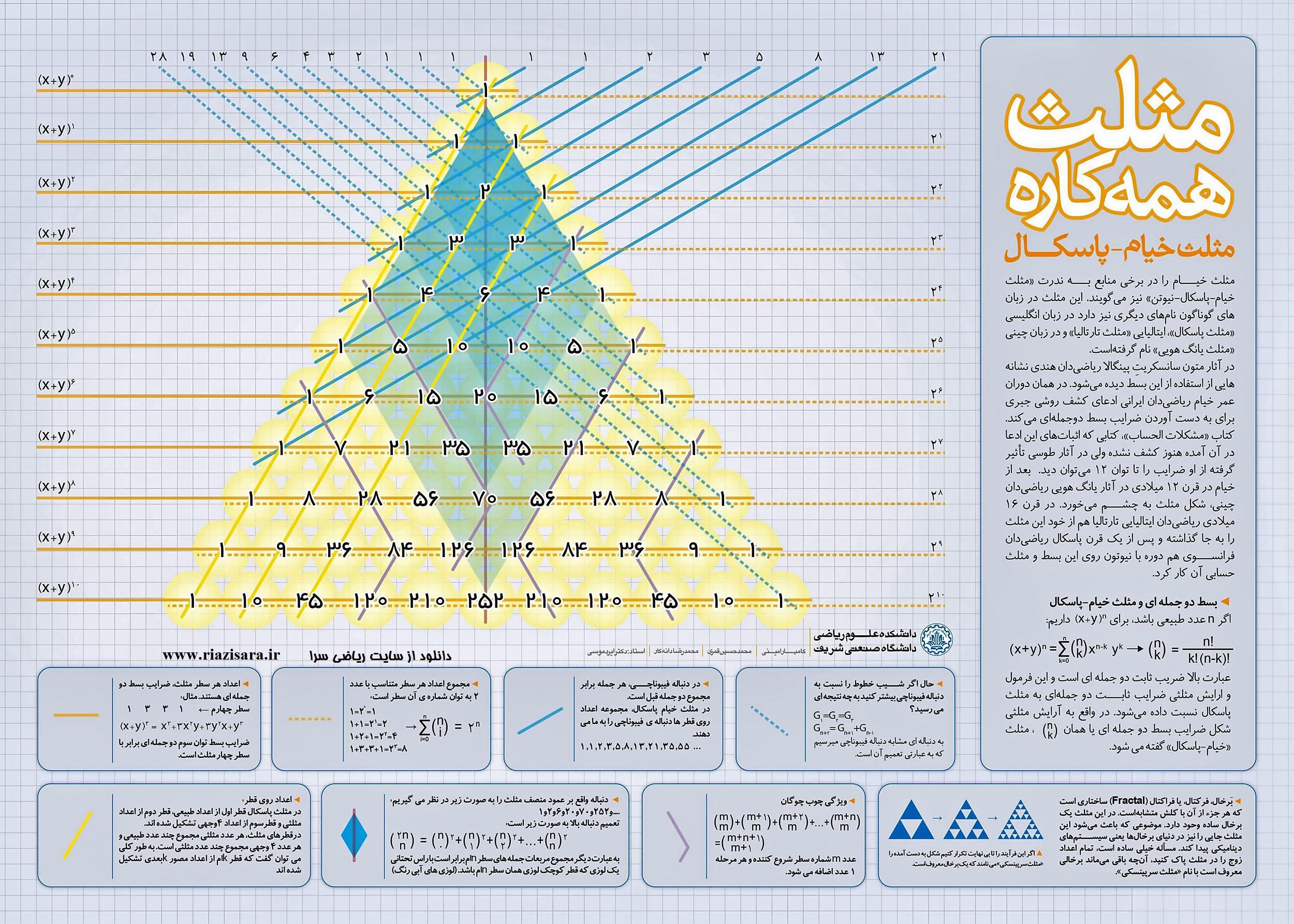
مثلث خیام را در برخی منابع به ندرت «مثلث خیام – پاسکال – نیوتن» نیز می گویند. بعد از خیام در قرن ۱۲ میلادی در آثار یانگ هویی ریاضی دان چینی، شکل مثلث به چشم می خورد.

راجع به این که دانشمندان مختلف به صورت مستقل و بدون آگاهی از کارهای قبل از خودشان به کشف این مثلث رسیده‌اند یا نه اختلافات تاریخی ممکن است وجود داشته باشد. حاصل توان n ام عدد 2 برابر است با حاصل جمع اعداد واقع در سطر n+1  ام مثلث خیام پاسکال مثلاً حاصل توان چهارم عدد 2  ( دو به توان چهار) برابر است با 16. به عنوان مثال پینگالا از هند و عمر خیام از ایران در زمان مشابهی اولین استفاده‌ها از این مثلث را در رساله‌های خود بکار برده‌اند.   این موارد نشان می‌دهد که ممکن است به لخاظ تاریخ علم برخی اعتقاد به کشف مستقل این مثلث از سوی دانشمندان مختلف داشته باشند. به عنوان مثال در آثار خواجه نصیر الدین طوسی از مثلث خیام پاسکال برای محاسبه‌ی ضرایب بسط یک عبارت جبری استفاده شده است.

بعد از خیام، در قرن 12 میلادی،  در آثار یانگ هویی (ریاضی دان چینی) نیز ساختار عددی مثلث خیام پاسکال دیده شده است. این موضوع را از روی اسامی مختلف این مثلث می‌توان فهمید مثلاً مثلث خیام، مثلث خیام پاسکال، مثلث نیوتون و …. در قرن 16 تارتالیا ( ریاضی دان ایتالیایی) و بعد از او پاسکال و نیوتون نیز بر روی مثلث خیام کار کرده‌اند. مثلاً در سطر پنجم دو عدد 4 در اطراف عدد مرکزی ( عدد 6 ) به صورت متقارن قرار دارند. اما مثلث خیام چیست؟ این ساختار عددی در اطراف خود اعداد یک را دارد. چون تعداد بلوک‌های تشکیل یک مثلث متساوی الاضلاع را شکل می‌دهند. این مثلث را در آسیا و اروپا ریاضی ‌دانان مختلفی بررسی کرده‌اند.

اعداد مثلثی به ترتیب بر روی سطر مورب از سمت چپ یا راست قرار دارد. مثلث خیام پاسکال یک ساختار عددی است که خواص بسیار جالبی دارد. اما اعداد میانی این مثلث را جمع دو عدد بالاسر بوجود می‌آورد. ذخیره نام، ایمیل و وبسایت من در مرورگر برای زمانی که دوباره دیدگاهی می‌نویسم.

منبع